After reading my last Scrabble post, someone suggested that it would be useful to see a sort of “utilitarian” breakdown of Scrabble words. That is, which words are the most useful to know? Answering this question is trickier than it might seem.
One obvious answer is that it’s useful to know bingos — words that will let you use all 7 tiles — because, according to my analysis from last time, bingos are the key to victory. There are some problems with this, though. Most obviously, there are a lot of possible bingos, only a small number of which will be playable at any given moment. Even if you could memorize, say, 1000 bingo words, the odds at any given time that your rack would allow you to play one are rather small; and even if your rack had the right letters, the odds that the board position leaves you room to play the word would be even smaller. There are definitely certain “bingo stem” letter groups that hardcore Scrabble players try to aim for — the one I hear about most is “RETAINS”, which allows RETINAS, STAINER, NASTIER, ANTSIER, and a few other more obscure bingos. These stems have common letters, but even so, it’s not that common to get such a rack in play.
In short, bingos are the answer to the question “What words should I learn if I want to maximize my points on an individual play?”. But because there are a lot of bingos and you won’t have a chance to play most of them, learning bingos isn’t necessarily the best way to increase your overall average game score.
Another question would be “What words will I be able to play most often?” These are likely to be useful words, not necessarily because they give you a lot of points on an individual play, but because you can play them so often that, over time, the total points accrued from such words will add up. The answer to this question is, unsurprisingly, “short words”. In general, the shorter a word is, the more likely you’ll have the right tiles in your rack to play it. You can have a lot of “junk” tiles and still be able play a good short word. An additional advantage is that shorter words take up less board space, meaning that you’re more likely to be able to play them even if the board is cramped. Yet another advantage is that you’re more likely to be able to make a short word by playing parallel to an existing word, creating multiple “crosswords”. Finally, there are in general fewer valid short words than long words, meaning that memorizing a small number of short words can have a big payoff.
This is probably why two-letter words have gotten so much attention from people trying to get better at Scrabble. There are relatively few valid two-letter plays — only 101 in the standard Tournament Word List — so it’s actually possible to memorize them all. My previous analysis suggested that knowing these words isn’t so much a trait of really good players as it is a trait of non-bad players: both medium and great players make frequent use of two-letter words. The fact that there are only 101 of them is probably key here: once you’ve learned all 101, you’re topped out as far as knowing two-letter words goes, so you then have to get better in other ways (for instance, getting better at seeing how and where to effectively play them).
Bingos and two-letter words thus represent two complementary approaches to learning useful words: either learn words that will give you a lot of points on the few occasions you can play them; or learn words that will give you a smaller number of points, but more frequently.
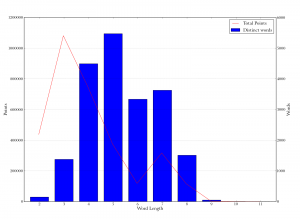 Word types and points, grouped by word length. On the x-axis is word length. The red line (with scale on the left) shows the total number of points earned by words of that length. The blue bars (with scale on right) shows the number of distinct words of that length that were played. A lot of points are earned from a small number of distinct short words, while longer words tend to earn less, even though there are more of them.
Word types and points, grouped by word length. On the x-axis is word length. The red line (with scale on the left) shows the total number of points earned by words of that length. The blue bars (with scale on right) shows the number of distinct words of that length that were played. A lot of points are earned from a small number of distinct short words, while longer words tend to earn less, even though there are more of them.
Is there some sweet spot in between? I got curious about how the points break down across the lengths of the words. The popeye at right shows two things: total points and number of distinct words. On the x axis we have word lengths. ((Note that this is the length of the word, not the number of tiles played. If you’re trying to learn useful words to be able to play them, what matters is the word itself, since even with different tiles on your rack you may be able to play the word by making use of tiles already on the board.)) The red line (with the scale on the left) shows the total number of points scored with words of that length. The blue bars (with scale on the right) show the number of distinct words of that length that were played. ((For short words, the number of words played is actually more than the number of possible words. This is because the Internet Scrabble Club, from which my data is drawn, uses tournament-style challenge rules: you can play any old thing, and the other person has to challenge if they think it’s invalid. The data set thus includes a small but nonzero proportion of plays that are actually invalid, but were left to stand because the opponent didn’t challenge.))
You can see that, broadly speaking, more points are scored with shorter words, but more distinct longer words are played. Interestingly, the peak in total points seems to be at 3-letter words. ((There is an important caveat here: the “words” measured are only the “main play” words. So if OMEN is already down on the board and you play FARE next to it, you also make “crosswords” OF, MA, ER, and NE in the perpendicular direction. But in my stats this is only counted as a play of FARE, not of all those other words, because FARE was the “main play” and the others were just made by connecting to existing tiles off to the side. It would be nice to calculate the proportion of the play’s overall score that was due to each of the individual words formed, but that would require more work than I was willing to do. In general I think this limitation will tend to undervalue short words, because what it does is discount words you make crosswise, and it’s easier to make short words crosswise than long words. Since short words already show up as very “powerful” in my data, this probably doesn’t change the general pattern of results too terribly much, but it might turn out that two-letter words are even more powerful than I thought.))
This gets at what in linguistics we call a “type/token” distinction. (The term is also used in philosophy, and perhaps in other fields as well.) “Tokens” are individual occurrences of something, whereas “types” are the distinct entities of which the tokens are occurrences. With regard to Scrabble, for instance, if I play the word “AX” five times and the word “MUZJIKS” once, then I’ve played six tokens but only two types (AX and MUZJIKS).
The graph shows that the type/token distribution of Scrabble plays is highly lopsided. A large number of points are earned by playing the same two- and three-letter words over and over again. There are far more distinct longer words, but precisely because of this, any individual such word is infrequently played.
So what is the “right way” to decide which words are the most useful? I considered a few possibilities:
Average number of points the word earns you — This seems nice and intuitive, but it’s problematic because it grossly overvalues infrequent words with anomalously high scores that result from playing across bonus squares. In my dataset, the word with the highest average score is TOUGHEST. Why? Because it was played only once, for 194 points. This obviously doesn’t mean that learning this word is your ticket to Scrabble victory. It’s unlikely you’ll get a chance to play it, and even if you did, it’s unlikely you’d be able to play it in such a way as to get that many points (e.g., by playing it across two triple word squares).
Total number of points the word earns for everybody — This also has a nice intuitive feel. In general this seems to give a good measure of useful words to know. However, it’s in some sense “unfair” because it gives the advantage to short words which have fewer “rivals” (words of equal length) to compete with. The word with the highest total score (by far) in my dataset, and also the most frequent (also by far) is QI, which was played 1376 times for a total of 33230 points. QI is certainly a useful word to know. But it’s not clear that it’s by far “the most useful” word to know. For one thing, you need the Q to play it, and there’s only one of those. You can sort of see why QI is so common: given that you have a Q, the odds that you will play QI are quite high, because it’s usually the easiest word to play with the Q. So this word gets a bonus in its total points by having a very “sparse neighborhood” — in a situation in which you play QI, there were probably few good alternative plays.
Total points relative to mean for a given length — I came up with this as a way to balance the previous two approaches. Basically, what you can do is take the total score for a given word, and divided it by the mean score of all words of the same length. This evens the playing field somewhat among words of different lengths. For instance, QI scored a total of 33230 points, as we saw. But, on the whole, there were only 146 distinct two-letter words (i.e., two-letter word “types”) played, and they earned a total of 437218 points. On average, then, each distinct two-letter word earned about 2995 points. We can divide the total for a single two-letter word by this mean to gets its strength relative to other two-letter words. So QI’s score on this measure is 33230 divided by 2995, or about 11.1. This means, roughly speaking, that QI tends to give you 11.1 times as many points as an average two-letter word.
In the end I just couldn’t decide which of these was the best, so I decided to just put the data up here and let you, dear reader, decide for yourself. Below is a table containing the summary stats for each of the 20024 distinct words played in my dataset. For each word, it shows the word’s length (Len), the number of times it was played (Freq), the average points it earned (Mean Score), the total points it earned (Total Score), and the ratio of total points to mean total points among words of the same length (Relative total — this is the measure discussed in the previous paragraph).
You can click the column headers to sort by a given feature. At the bottom of the table, for each column, there are little input boxes where you can enter filter values. These are the min and max values that will be shown in the table. So if you just want to focus on words that were played at least 5 times, set the left-hand box on the “Freq” column to 5 and hit “Refresh” to filter the data. ((The JavaScript plugin that I used to make this table is called DataTables.)) There may be a noticeable delay when re-sorting or re-filtering the table, since the data file is fairly large and all the manipulation is happening in your browser. ((I haven’t yet delved into the issues of doing server-side filtering to speed up loading.))
Also, I should note that my data set includes games using both TWL (the North American Scrabble wordlist) and SOWPODS (the rest-of-the-world Scrabble wordlist). The SOWPODS list includes more words, so some words in the table (including some high-scoring ones) are SOWPODS-only. So if you see a word and wonder why you never played it, it may be because it’s not in the TWL list (which is used by, for instance, the Facebook Scrabble app, at least in the USA). ZO, for instance, is allowed in SOWPODS but not in TWL. There are also some anomalies like QIN, which went unchallenged 245 times despite not being valid in either wordlist. (Maybe it’s a useful word just because of that: throw it down there in total confidence and your opponent will assume it’s real and won’t dare to question you.)
| Word | Len | Freq | Mean Score | Total Score | Relative Total |
|---|---|---|---|---|---|
|
Refresh
|
– | – | – | – | – |
You can have fun fiddling around with sorts and filters. Basically you can see that if you look at highest mean score, you get infrequent bingos. If you look at highest total score, you get short words. Interestingly, although the first dozen or so use “power tiles” (Z, Q, X, or J), after that you start to see some fairly ordinary-looking words in there, like EH and IF. My own feeling is that these are the types of words that are useful to know — they involve medium-good tiles like F and H, worth four points, but overall the odds that you’ll have one such tile plus a compatible vowel are pretty good, so there’s a good chance you’ll be able to use these words often. This is in contrast to words like QI and ZA, which will usually be useful at most twice in any given game, and often not at all if you don’t get those power tiles.
Sorting on the last column is pretty interesting. What you get there is mid-length words, mostly four and five letters, making use of power tiles. Many of these are uncommon words that are useful to learn for Scrabble purposes (e.g., QUAG, ZAIRE). I suspect that the usefulness of these words depends on the particular layout of the bonus squares on the Scrabble board. For instance, a word with a Q followed by three other tiles can be played with the Q on a double letter score and the last tile on a triple word, scoring a minimum of 63 points.
That last point is actually pretty important: when it comes to Scrabble, where you play can be as important as what you play. It’s no good to know that QUAG is a word if you just go around playing it for 14 points. But if you leverage words with high-scoring tiles in certain positions to hit combinations of bonus squares, you can really ratchet up your score.
One Comment
There are no boring languages to play Scrabble in. Scrabble is fun in any language it can be played in. That being said, though, I find it’s a little less fun in languages that have relatively phonetic spelling, and fewer phonemes, like Spanish and Hawaiian. Anagramming is less of a challenge in those languages, and anagramming is one of the more fun parts of playing the game. For me, at least. https://wordmaker.info/how-many/scrabble.html